1 核心思想
random sampling and data coherence
2 算法目的
quickly finding approximate nearest neighbor matches between image patches
3 问题描述
给定两张图像A B, 对图像A中的每个patch,找到图像B中与之匹配度最高的patch.
3.1 一些定义
- NNF(nearest-neighbor field)
定义NNF为$f: A \rightarrow R^2$,假如图像A中的patch a与图像B中的patch b对应, $f(a) = b - a$, patch的坐标使用patch中心的坐标代替,同时需要定义距离函数$D$。
4 算法步骤
问题简化为:为图像A中的每个patch a计算f(a)的值
4.1 initialization 初始化
为图像A中的每一个patch a赋值随机的f(a)
(在图像B中进行独立的均与采样(independent uniform sampling))
- 或者使用prior information
- 迭代
接下来的需要对每个像素迭代进行propagation和random search来改进f(a)的值, 遍历像素的顺序为从左到右,从上到下,且不是所有像素都完成propagation后进行random search,而是对每一个像素进行完propagation后立刻进行random search。
4.2 propagation 传播
利用$f(x-1, y)$和$f(x, y-1)$的值来改进$f(x, y)$
$f(x, y)$的新值是$min(D(f(x,y)), D(f(x-1, y)), D(x, y-1))$对应的$(x,y)$
- $D$为距离函数
- 在偶数次迭代可以使用从右往左,从下往上的顺序迭代
4.3 random search 随机搜索
$u_i = v_0 +wa^iR_i$
$v_0 = f(x, y)$,$R_i$为$[-1,1]\times[-1,1]$,$w$为搜索窗口大小,$a_i$为每次搜索窗口衰减的比例
即以f(x, y)为中心的window进行搜索
- 停止条件即搜索半径小于等于1个像素:$wa^i < 1$
5 一幅图说明
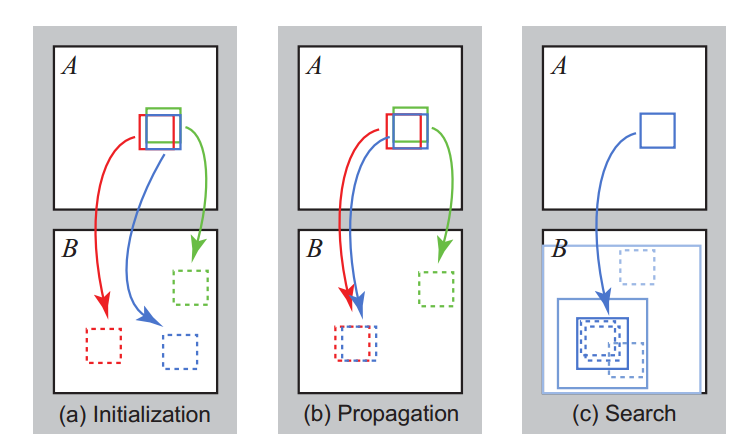
约定: 下文称f(a)为a的offset
需要搜索A图像中蓝色patch的offset, 红色patch是蓝色的left patch, 绿色patch是蓝色patch的up patch。
在( a )initialization中可以看到A图中3个颜色的patch被赋予了B图中随机的offset。
在( b )proagation中检查红色patch和绿色patch在B图中的offset是否比蓝色patch的offset更加match,可以看到红色的ofset更加match,于是更新蓝色patch的offset。
在( c ) random search中,以( b )中更新的offset为中心的window进行随机搜索。
重复( b )( c )步骤直到收敛。
6 GPU实现
思路: propagation和random search阶段并行。
矛盾: propagation之前的CPU version是以scanline的形式进行,这意味着propagation是有先后顺序。
解决方案: jump flood scheme
7 分析
假设图像A B都是M像素,考虑所有像素都被初始化到错误的offset的概率为$(1-1/M)^M$, 则至少有一个像素被初始化到正确的offset的概率为$1 - (1-1/M)^M$
M很大的时候近似为$1 - 1/e$。
由于在random search阶段的时候,在小的邻域范围内的搜索是很密集的,可以认为只要在正确的offset一定领域内的offset都可以认为是正确的。
基于以上的考虑,propagation和random search可以大大加速算法的搜索速度。
8 参考
PatchMatch: A Randomized Correspondence Algorithm for Structural Image Editing