1 认识几个坐标系

世界坐标系
物体在真实世界中的位置
相机坐标系
物体在以相机为原点的坐标系中的位置
成像坐标系
在二维成像平面的位置
像素坐标系
在实际数字相片中的坐标只有最后一个坐标系的单位是px，为实际图像中的坐标位置，比如1080 * 720的图像就可以看成一个以图像左上角为原点建立的坐标系。

1.1 世界坐标系 -> 相机坐标系

$\left[ \begin{matrix} x\\ y\\ z \end{matrix} \right] = \left[ \begin{matrix} R & T\\ 0 & 1 \end{matrix} \right] \left[ \begin{matrix} X\\ Y\\ Z\\ 1 \end{matrix} \right] \tag{1}$

R是3 * 3 的旋转矩阵 T是3 * 1的平移矩阵

0是1 * 3 的全部为0的矩阵 1为1 * 1的矩阵

所以可以看到4 * 4的变化矩阵乘以4 * 1的齐次坐标，结果应该为4 * 1的齐次坐标，这里结果为3 * 1是因为丢掉了齐次坐标中的最后为1的那个维度。

$\left[ \begin{matrix} R & T\\ 0 & 1 \end{matrix} \right]$

矩阵也称为外参矩阵/相机的位姿

1.1.1 为什么需要齐次坐标呢？

就是为了能用一个矩阵表达变化，后面不需要齐次坐标了所以可以丢掉最后一维。

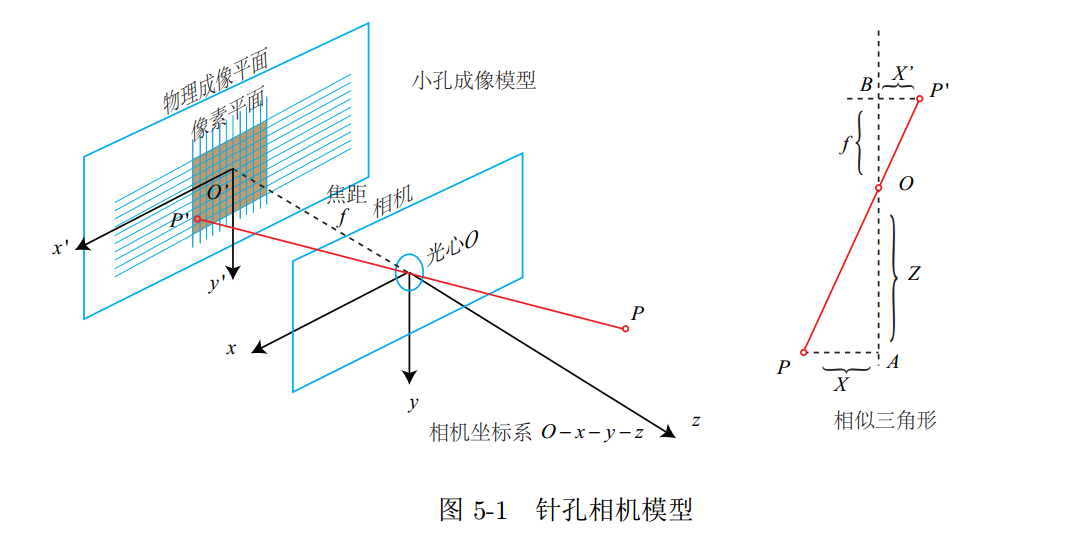
1.2 相机坐标系->成像坐标系

$\left[ \begin{matrix} x/z\\ y/z\\ 1 \end{matrix} \right]$

相当于投影到了相机坐标系中$z = 1$的平面

1.2.1进行正畸

几种畸变

径向畸变
- 透镜本身缺陷
桶形畸变
- 由于透镜摆放位置不平行光圈

1.3 成像坐标系->像素坐标系

$\left[ \begin{matrix} u\\ v\\ 1 \end{matrix} \right] = \left[ \begin{matrix} f_x & 0 & c_x\\ 0 & f_y & c_y\\ 0 & 0 & 1 \end{matrix} \right] \left[ \begin{matrix} x_{corrected}/z\\ y_{corrected}/z\\ 1 \end{matrix} \right]$

其中

$\left[ \begin{matrix} f_x & 0 & c_x\\ 0 & f_y & c_y\\ 0 & 0 & 1 \end{matrix} \right]$

也被称为为相机的内参矩阵

成像平面的坐标系的原点是在中心的，而像素平面的原点是在左上角的，向右边是u
向下是v，u和v的单位都是px

内参矩阵相当于进行了二者的一个映射，即先乘以分辨率进行放缩，然后加上偏移量移动原点

2 相机标定

相机标定需要确定的参数个数为9个
$(f_x, f_y, c_x, c_y, k_1, k_2, k_3, p_1, p_2)$
同时我们需要关注的是成像坐标系 -> 像素坐标系，这里是内参矩阵作用的地方

对于K个棋盘照片，每一个棋盘中的N个角点，我们都有一个x, y的坐标，也就是我们能够得到2NK个等式

K个棋盘照片意味着有K个相机的位姿，即K个外参矩阵，也就是6K个参数。
同时相机内参有4个参数，这意味着一共有6K + 4个参数。

$2NK > 6K + 4$ $NK > 3K + 2$ $K(N-3) > 2$

2.1 如何确定标定板的三维坐标

根据K个棋盘照片，我们可以求得每个角点的像素坐标

然后我们可以以标定板所在平面为z=0的平面建立世界坐标系，同时设定相邻角点的坐标差，就可以得到所有角点在世界坐标系下的坐标。

(世界坐标系嘛…人为设定一下就好)